Abstract
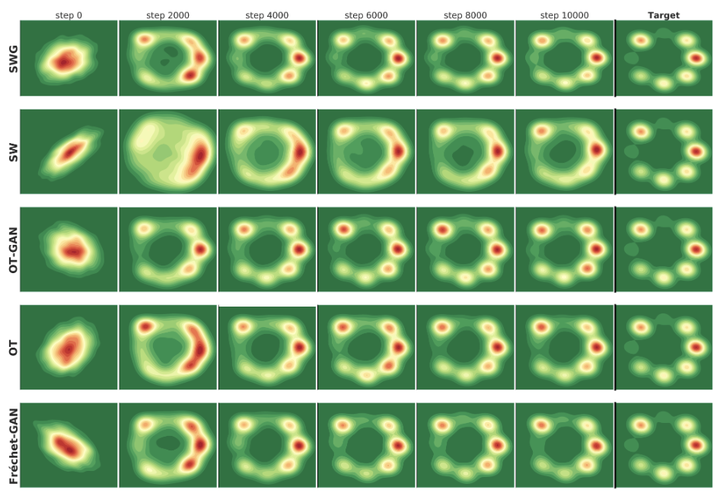
For a given image generation problem, the intrinsic image manifold is often low dimensional. We use the intuition that it is much better to train the GAN generator by minimizing the distributional distance between real and generated images in a small dimensional feature space representing such a manifold than on the original pixel-space. We use the feature space of the GAN discriminator for such a representation. For distributional distance, we employ one of two choices; the Frechet distance or direct optimal transport (OT); these respectively lead us to two new GAN methods; Frechet-GAN and OT-GAN. The idea of employing Frechet distance comes from the success of Frechet Inception Distance as a solid evaluation metric in image generation. Frechet-GAN is attractive in several ways. We propose an efficient, numerically stable approach to calculate the Frechet distance and its gradient. The Frechet distance estimation requires a significantly less computation time than OT; this allows Frechet-GAN to use much larger mini-batch size in training than OT. More importantly, we conduct experiments on a number of benchmark datasets and show that Frechet-GAN (in particular) and OT-GAN have significantly better image generation capabilities than the existing representative primal and dual GAN approaches based on the Wasserstein distance.